

こんにちは、カイトです。
F=ma
みなさんは、これが何を表す式か、わかりますか??
運動方程式じゃないの?
このように考えたかた、もちろん正解です。
しかしこの式、見方によっては、力のつり合いの式だとみることが出来ると考えたことはありますか?
この記事では、F=maを題材に、運動方程式と力のつり合いについて、お互いの関係性についてしっかり解説していきます。
この記事で学べること。
・運動方程式と力のつり合いについて、お互いの関係がわかる。
・慣性力に対する理解が深まる。
・力学で式を組み立てるときに、意味が分かる。
・(大学生向け)システム制御における、動的/静的システムの理解につながる。
目次
まずはそれぞれの定義を確認。
まずは、それぞれの定義を見てみましょう。
運動方程式
まずは、運動方程式についてみていきます。
学研キッズネットさんが、非常にわかりやすい定義づけをしていたので、ここから引用させていただきます。
物体の運動のようすを定める方程式。ニュートンの運動の第2法則によると,物体の質量m と加速度a の積は,この物体に作用している力F に等しいので,F = ma の方程式がなりたつ。
学研キッズネット

この記事を読んでいる人ならば、当たり前だと感じることだと思います。
では、Fとaの向きはどうなるでしょうか。
メモ
物理を学んでいく上では、大きさと向きが非常に重要なファクターになっていきます。
文字をおいて立式した場合、その大きさだけでなく、向きについても目を向ける癖をつけましょう!
ここでは右向きを正として、加速度aを置いてみましょう。
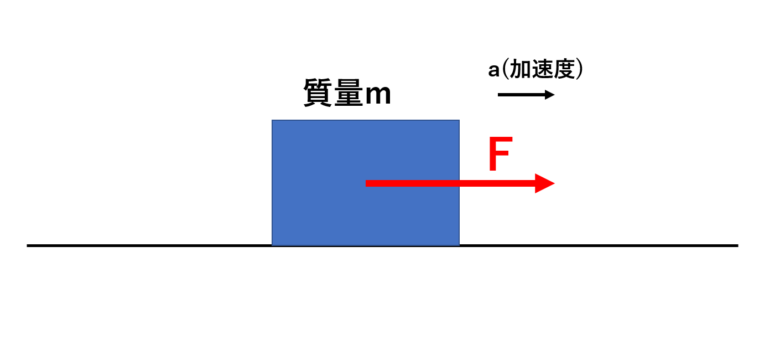
そうするとどうですか? この力Fも右向きと定義できますよね。
なぜなら、外力によって加速度が発生するからです。
モノを引っ張ったら、その向きに加速度は発生しますよね?

例えば電車が発車したとすれば、進行方向(力が加わった向き)と加速度の向きは一致するはずです。
当たり前すぎて、教科書にも載っているか怪しいですが、この感覚も大切です。
さて、上ではFを“この力”と表現しましたが、“この力”はどのような力と言えるでしょうか。
この力Fは物体に働く力(ある意味では、外力)であると言えます。
この運動が起こるためには、加速度aが必要ですよね。
この加速度ですが、加速度は何かしら外から力を受けないと大きくなったり小さくなったりしません。
誰かが物体を押す/摩擦力が働く/傾斜の上を走る etc

当たり前ですが、外部から力Fを加えたことで加速度aが生じてる、このような関係がFとaにはあります。
それでは最後に、この式はどこから見た式でしょうか。
(この式を立てるうえでの視点はどこでしょうか?)
答えは、この運動系の外ですね。
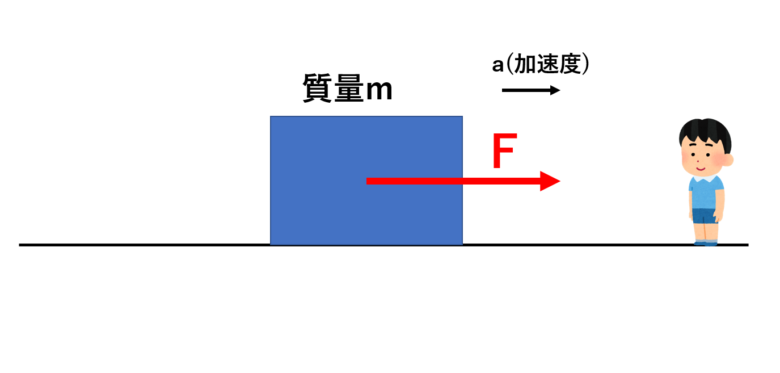

動いている電車での運動に例えるならば、この動いている電車を外からの視点が、運動方程式の視点になります。
ここまで理解できれば、OKです。
続いては力のつりあいを見ていきましょう。
力のつり合い
同様に学研キッズネットから、力のつり合いの意味を引用しました。
1つの物体にいくつかの力が同時にはたらいていて,物体が静止しているとき,これらの力はつり合っているという。
学研キッズネット

これも、当たり前の話ですよね。
このつり合いを考えるうえで大切なのは、真逆の向きの力の大きさは等しいということ。
右向きの力=左向きの力
あるいは、
上向きの力=下向きの力
と言った方がわかりやすいかもしれません。
静止している物体に対して、この式が成り立つのが、力のつり合いです。

静止している、というのが力のつり合いのキーポイントです。
二つの違いは?
2つの違いは、加速度を持っているか否かである。
ここまで二つの現象を見てきましたが、2つの違いに気づきましたか?
違いは、物体に加速度がかかっているか否かですね。
- 静止している物体→力のつり合い
- 加速度をもって動いている物体(の運動)→運動方程式

等速で動いている物体に関しては、その物体自身にかかる加速度はゼロですから、力のつり合いが成り立っています。
それでは冒頭に話を戻します。
加速度を持っている、F=maをどうやって力のつり合いで表わせばいいのでしょうか。
視点を変えてみる。
ここで重要になってくるのが、慣性力という概念です。
ニュートンの運動の法則がなりたつ座標系(慣性系)に対して加速度a で運動している物体を,物体とともに運動する座標系(非慣性系)から見ると,つねに静止して見える。
学研キッズネット
先ほどの、例に戻りましょう。

この動く物体の運動に関して、物体の上に乗った人からの視点で運動を見てみるとどうなりますか。

動いている電車での運動に例えるならば、この動いている電車の中(乗客)からの視点を言っています。
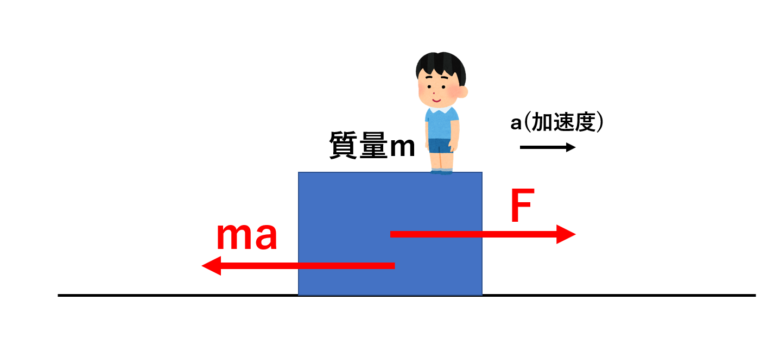
電車の中の人は、加速度の大きさにかからわず、静止していますよね。
静止しているということは、つり合いの式が成り立つはずです。
静止しているということは、今右向きにFが働いているので、その力と逆向きで同じ大きさの力が働かないといけないですよね。
このように、視点を加速度運動してる物体に変えた時に、仮想的に働いているとみなしている力を慣性力と呼びます。
そして逆に言えば、加速度運動している物体に視点を移せば、力のつり合いが成り立つと言えるわけです!!
【発展(大学生向け)】システム制御での、動的/静的システムの式を立ててみる。
ここはおまけです。
そもそも僕がこの疑問にぶち当たったのが、システム制御における、マス・ばね・ダンパーシステムを考えるときに力の向きと加速度がごっちゃになったのが原因でした。
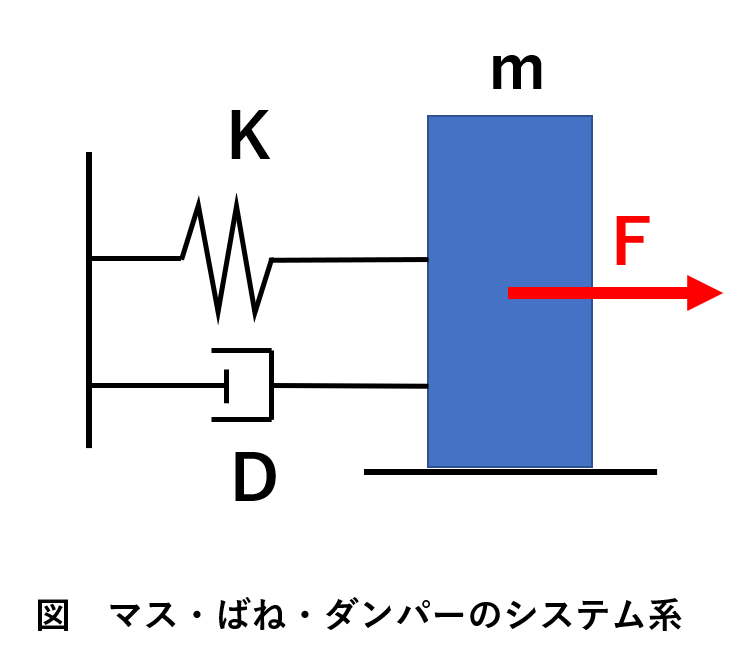
ただ、これも状況を整理すれば式の意味が分かります。
まず、ここでいうFは外力です。
このシステム系を動かす(動かし続ける)ために、外力Fを加えるわけです。
ここで、これを運動方程式としてみるとどうなるでしょうか。
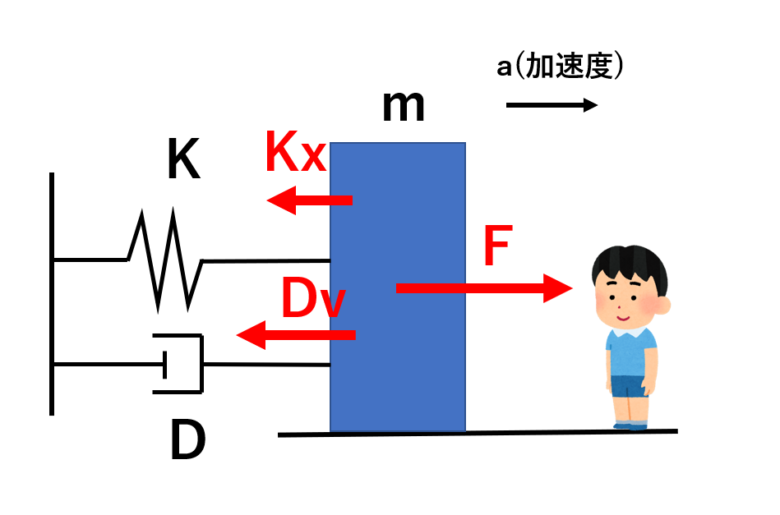
この物体にかかる、運動方程式は、
ma=F-Kx-Dv
になります。
一方で、物体からの視点で考えるとどうなりますか?
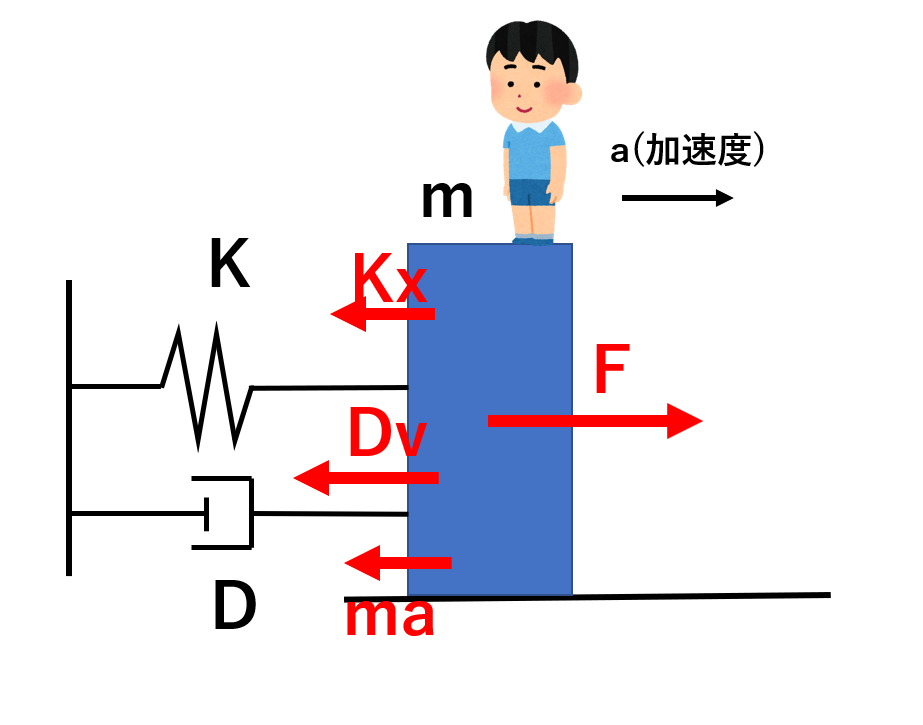
力のつり合いから、
F=ma+Kx+Dv
になりますよね。
そしてこの2つの式はもちろん同じです。
物理的には意味は違いますが、同じ現象を見ているので、式が一致するのは当たり前ですよね。

より正確に言えば、一致するために、慣性力を導入しているわけですが…。
力のつり合いと運動方程式をしっかり理解出ていれば、こういった少し複雑なシステム系でもしっかり理解することが出来ます。
まとめ。
まとめるとこんな感じです。
まとめ
・運動方程式は、加速度をもって運動をしている場合に使う。
・力のつり合いは、静止している(加速度がない)時に使う。
・運動方程式も、視点を変えることで、力のつり合いとみなすことができる。
この記事で書いてあることは、物理の力学を解くうえで基本中の基本です。
なので多くの人は、何を当たり前のことを言っているのだ?と思う部分が多かったと思います。
むしろ、こういった部分でつまずくのは、中級者ではないかと感じます。
力学の式は直感でわかる部分も多いですよね。
だからこそ、何となくで理解していた人が、問題演習をしたり、現象を深く考えていく過程で沼にはまっていく印象を受けます。

僕自身、大学4年生になって、この沼にはまりましたからね。恥ずかしい限りです。
みなさんは僕のようにならないように、物理現象で少しでも疑問に思ったら、すぐに解決する癖をつけましょう!