

こんにちは、カイトです。
この記事では、電磁気を勉強するうえで重要な、電束について丁寧に解説しています。
この記事で学べること。
・電束の意味が分かる。
・電束と電気力線、電束と電束密度との関係性がわかる。
・電束密度と電界との間のイメージがつかめる。
目次
電束の言葉の意味。
まずは式を使わず、言葉の意味を考えてみましょう。

電束というと、電気の束ってことかな…?
言葉通りに理解しようとすれば、こういうことになりますよね。
抽象的な表現ですが、簡単に言えば、
電束は、電気力線をεごとにまとめた束だとみることできます。
ここで電気力線が出てきましたが、電気力線と電束はどのような関係にあるのでしょう?
次章で一緒にみていきましょう。
電束は電気力線を使ってどのように表される?
まずは電気力線について、軽く復習しておきましょう。
参考
ファラデーは静電界が作用する理由として、正負の電荷の間に、目に見えない線が張られており、クーロンの法則による力はこの線に沿って作用すると考えました。
この空間に微小な正の電荷を置けば、電荷は電場から力を受けて動きます。
そしてこの電荷の動きに沿って線を引けば、空間に1本の線が描けます。
この線を電気力線と呼び、空間に存在する電気力線の本数は、N[本]として表します。
この電気力線は、空間によって変わる誘電率εを使って、
N=Q/ε (Q:電荷の大きさ ε:誘電率)
で表せることは、すでに学校で習ったと思います。


この式の肝は、εで割っているという部分です。
たとえ同じ大きさの電荷でも、置かれた空間によって、電気力線の本数は変わってくるのに注意しましょう。
前の章では、
電束は電気力線をε本ずつ束ねた束と言える。
と書きました。
ということは電束は、
N×ε=Q
となることがわかりました。
電束を考えるうえでのポイントは、周囲の空間における誘電率εに依存しないという点です。(Qで一定である。)

この、電束が誘電率εに依存しないで決まるというのが、電界Eを考えるうえでも非常に役立つんです。
(詳しくは次章でまとめます。)
それでは、最後に電束と電気力線の関係をまとめましょう。
電気力線:Q[C]からQ/ε[本]の電気力線が出ている。
→周囲の媒質の影響を受けている。
電束:Q[C]からQ[本 or C]の電束が出ている。
→周囲の媒質に寄らず、一定になる。
より厳密に電束についての定義は応用編を確認してください!
続いて、電束密度Dと電界の関係を見ていきます!
電束と電束密度、電界の関係を確認!
まずは、電束密度について軽くまとめます。
電束密度は、言葉通りに考えれば、
単位面積当たりの電束のこと
(ただし、基準の面を垂直に通過した成分の電束を考える。)
と表すことが出来ますね。

まずは、これくらいの認識で十分です。
では、この電束密度Dと電界Eの関係はどうなるでしょうか?
電束密度Dと電界Eは、誘電率εを用いて、
D=εE
の式で結びつけられます。

この式の意味は何でしょうか??
先ほど僕は、電束は誘電率εの値に寄らずに一定と書きました。
ここから単位面積当たりの電束である電束密度も誘電率εの値に寄らず一定なのはわかると思います。
D=εEの式は、
電気力線が通過する物質によって大きさが変わる電界Eに対して、電束密度は一定であるということを式で示している
と言えます。


イラストで見ると、イメージしやすいでしょうか。
任意の空間において、Eとεの積は必ず一定になることが、このイラストからもわかっていただけたと思います。
(つまり、Eとεは反比例の関係と言えます。)
最後に、電束密度と電界の違いをより明確に比較するために、ガウスの法則を用いて電束と電気力線を導きます。
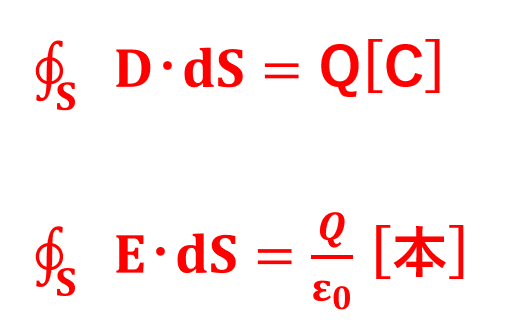
・ガウスの法則を用いて、電束密度Dを任意の閉空間で面積分すると電束になります。
・ガウスの法則を用いて、電界Eを任意の閉空間で面積分すると電気力線の本数を求めることが出来ます。

電束は、電束密度、電界、電気力線とも密接に関わり合っているんですね。
色々式が出てきて、少し混乱してきた人も多いと思います。
最後に、電束と電束密度、電界、電気力線の関係をまとめます。
電束・電束密度・電界・電気力線の関係をまとめる。
電束、電束密度、電界、電気力線について、相関関係を一つの図にまとめてみました。


これを見ただけでも、だいぶすっきりしたと思います。
ここまで読んできて、
万能(すべての誘電率で一定)な電束密度があるのに、なんでわざわざそこに真空の誘電率を掛けた値を電界として置きなおしたのだろう?
と思われた方がいるかもしれません。

電界を電磁気学にわざわざ導入する必要なのか?
答えは簡単、そもそも電界は別概念だからです。
みなさん、電界の定義を思い出してみてください。
電界(電場)とは、帯電した物体の回りに存在し、その電荷に働く力の存在する領域と考えます。
KEYENCE|帯電のメカニズムと計算方法
今回は電束について解説した記事なので、電界と電束密度の関係性にフォーカスばかりしていました。
しかし電界の本質的な単位はV/mで、
電圧が点電荷からの距離に反比例する
ことを表していました。
この電界が、電束密度を真空の誘電率で割った値と一致する、というイコール関係が物理的に大切だということです!
【補足】電気力線の本数=電束とする参考書もある。(レア)
僕が電束について勉強していく上で、『ベーシック電磁気学 / 著.川辺哲次 (裳華房)』では、電束を電気力線の本数として定義していました。

この参考書では終始、電束:ψ=Q/εと書かれていて、僕はずっと頭を悩ませていました……
正直、この参考書以外にこのような定義づけをしている文献は見たことありませんが、こういう置き方をされる可能性もあるということを頭に入れておくと、良いでしょう。
まとめ。
非常に長くなりましたが、ようやくまとめです。
まとめ
・電束は周囲の媒質によらず一定である。(電気力線は、周囲の媒質によって変化する。)
・電束は、電束密度をガウスの法則で面積分すると得られる物理量である。
・電界と電束密度は、誘電率εで結びつけられる。(D=εE)
僕自身もこの記事をまとめる段階で、色々な文献をあたりながら電束についてだいぶ深い理解を得ることが出来ました。
この記事がみなさんの電束への理解の助けになれば幸いです!
参考図書
・要点がわかる 電磁気学 / 著.石井望 (コロナ社)
・ベーシック電磁気学 / 著.川辺哲次 (裳華房)
・裳華房テキストシリーズ・物理学 電磁気学 / 著.兵頭敏夫 (裳華房)