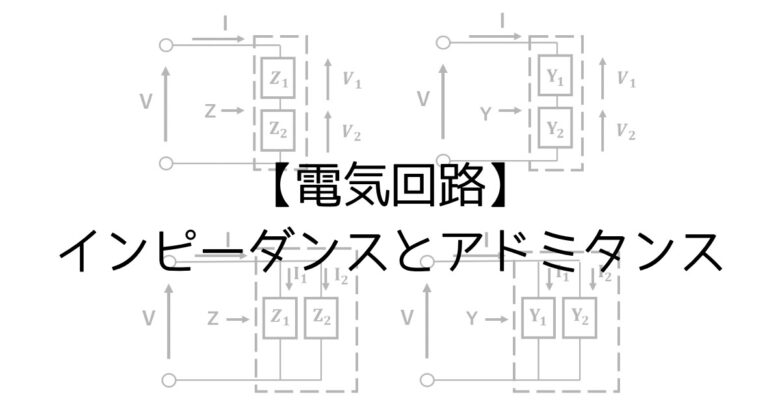

こんにちは、カイトです。
この記事ではまず、インピーダンスとアドミタンスでの直列接続・並列接続について、両者を比較しながらまとめていきたいと思います。
メモ
それぞれの性質については、以下の記事を参照してください。
その上で、以下の4パターンに分けてそれぞれの状況に関して具体的な問題を通して間違いやすいポイントを解説します。
今回取り扱う4つのパターン
①直列接続のインピーダンス。
②並列接続のアドミタンス。
③直列接続のアドミタンス。
④並列接続のインピーダンス。
しっかりと電気回路の勉強をしている人は、①と③、②と④は本質的に同じ事じゃん!と感じるはずです。
ただし、ここではこの違いをより明確化するためにあえて分けて触れることにします。
ぜひ最後まで読み進めて、すべての違いを完璧に理解しましょう!
この記事でわかること
・インピーダンス・アドミタンスの違いがわかる。
・直列・並列でどちらを考えればいいかがわかる。
目次
インピーダンス・アドミタンスの直並列接続。
まずは、インピーダンス・アドミタンスの直並列接続の特徴をまとめます。
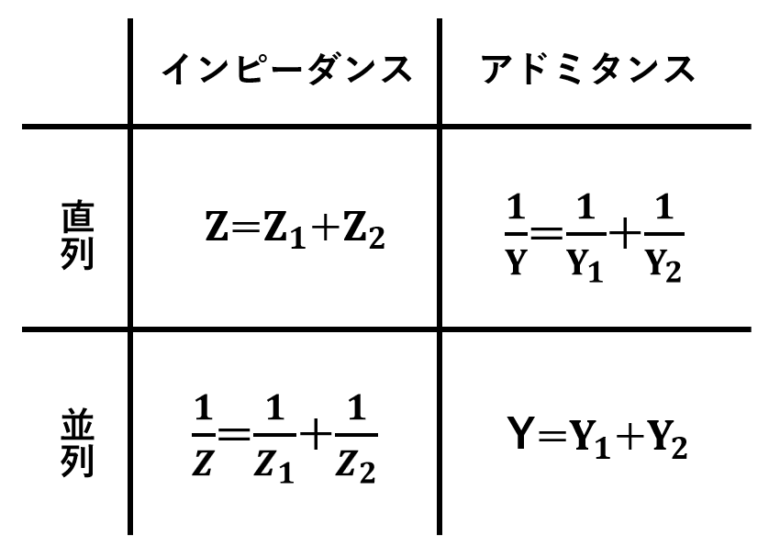
この表からもわかるように、直列接続ではインピーダンスを、並列接続ではアドミタンスを考えると考えやすくなります。
ポイント
直列接続ではインピーダンスを、並列接続ではアドミタンスを考えると良い。

仮に、「この直列接続回路の合成アドミタンスを求めよ。」という問題だとしても、先に合成インピーダンスを求めてからアドミタンスに変換した方が確実に計算ミスが減るので、上のルールに従いましょう。
ここからは、4つのパターンについて具体的な問題を通して解説していきます。
【パターン①】直列回路のインピーダンス。
まずは、直列回路のインピーダンスです。
条件
\(Z_1=R_1+jX_1\)と\(Z_2=R_2+jX_2\)の素子が直列で接続されたときの合成インピーダンスを求める。
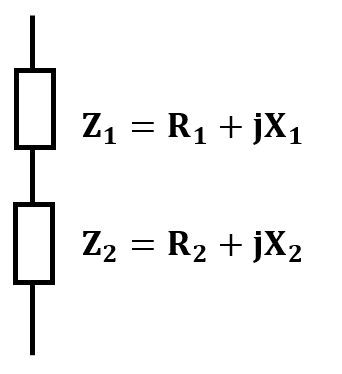
このとき合成インピーダンスは、
$$Z=Z_1+Z_2$$
なので、
$$\color{red}{Z=(R_1+R_2)+j(X_1+X_2)}$$
になる。
例題を解いてみましょう。
例題1
\(R\)と\(-jX_c\)を直列につないだときの合成インピーダンスを求めよ。
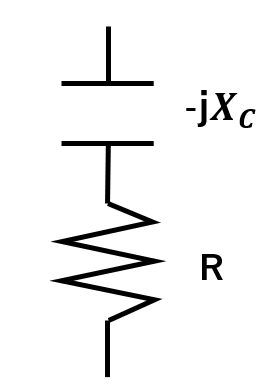
手順通り考えて、
$$\color{red}{Z=R-jX_c}$$
である。
ポイント
直列接続のインピーダンスはそのまま足し合わせる!
【パターン②】並列回路のアドミタンス。
続いて、並列接続のアドミタンスです。
条件
\(Z_1=R_1+jX_1\)と\(Z_2=R_2+jX_2\)の素子が並列で接続されたときの合成アドミタンスを求める。

この時の合成アドミタンスは、それぞれの素子のアドミタンスを先に出しておくことで、その足し合わせで出せます。
$$Y=Y_1+Y_2$$
なのでまずはそれぞれの素子のアドミタンスを求めます。
$$Y_1=\frac{1}{Z_1}$$
$$Y_2=\frac{1}{Z_2}$$
より、
$$Y_1=\frac{1}{R_1+jX_1}$$
$$Y_2=\frac{1}{R_2+jX_2}$$
を得ます。
合成アドミタンスは、
$$\color{red}{Y=\frac{1}{R_1+jX_1}+\frac{1}{R_2+jX_2}}$$
である。
分母を有理化して整理すると以下の式を得ます。
$$\color{red}{Y=(\frac{R_1}{R_1^{2}+X_1^{2}}+\frac{R_2}{R_2^{2}+X_2^{2}})−j(\frac{X_1}{R_1^{2}+X_1^{2}}+\frac{X_2}{R_2^{2}+X_2^{2}})}$$

非常に複雑な式になりましたが、これは一般形なので頭に入れて置く必要はないです!
それでは例題を解いてみましょう。
例題2
\(R\)と\(R_L+jX_L\)を並列につないだときの合成アドミタンスを求めよ。
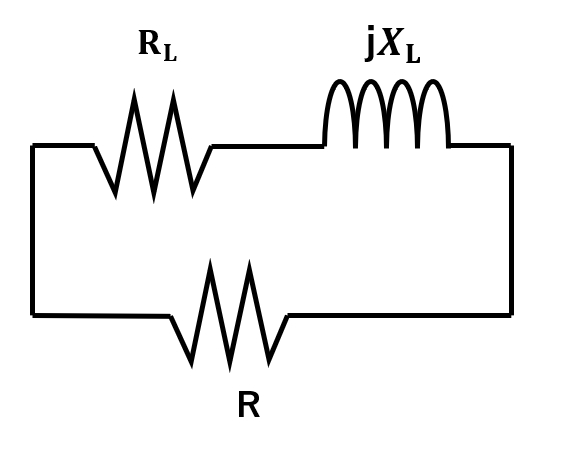
手順通りまずはそれぞれのアドミタンスを求めます。
$$Y_1=\frac{1}{R}$$
$$Y_2=\frac{1}{R_L+jX_L}$$
なので合成アドミタンスは、
$$Y=\frac{1}{R}+\frac{1}{R_L+jX_L}$$
$$\color{red}{Y=(\frac{1}{R}+\frac{R_L}{R_L^{2}+X_L^{2}})-j\frac{X_L}{R_L^{2}+X_L^{2}}}$$
になる。
ポイント
並列接続のアドミタンスはそのまま足し合わせる!
【パターン③】直列回路のアドミタンス。
続いて考えるのは、直列回路のアドミタンスです。
条件
\(Z_1=R_1+jX_1\)と\(Z_2=R_2+jX_2\)の素子が直列で接続されたときの合成アドミタンスを求める。
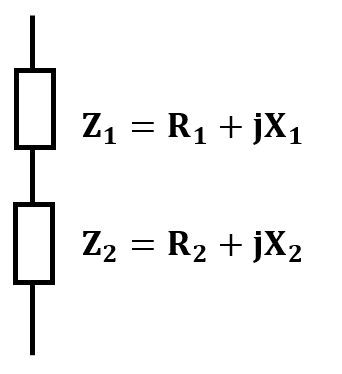
メモ
これは前述の通り、直列回路のインピーダンスを考えるのと本質的には同じですが、あえて分けて考えてみます。
直列接続の合成アドミタンスの式は、
$$\frac{1}{Y}=\frac{1}{Y_1}+\frac{1}{Y_2}$$
なので、まずはそれぞれの回路のアドミタンスを考えます。
それぞれのアドミタンスは、
$$\frac{1}{Y_1}=Z_1$$
$$\frac{1}{Y_2}=Z_2$$
となります。
直列回路のアドミタンスの式に代入すると、
$$\frac{1}{Y}=Z_1+Z_2$$
となりますよね。
なので、合成アドミタンスは、
$$\color{red}{Y=\frac{1}{Z_1+Z_2}}$$
で表せます。
ただこのやり方、逆数の形が何度も出て、正直かなりミスを誘発します。

僕自身、「直列接続の合成アドミタンスを解け」というタイプの問題を初見で解いたとき、分母分子がぐちゃぐちゃになり、間違えてしましました。
なので、このタイプの問題は、まず合成インピーダンスを求めて、最後に逆数を取ることを強く勧めます。
ポイント
直列接続の合成アドミタンスを解く際は、まず合成インピーダンスを求めるべし!
それでは、僕が実際に問題演習の際に間違えた問題を下の例題で出しますので、是非手を動かして考えてみましょう!
例題3
\(R[Ω]\)の抵抗と\(C[F]\)のコンデンサを直列につないだときの合成アドミタンスを求めよ。
ただし、電源は交流電圧源とし、周波数はωとする。
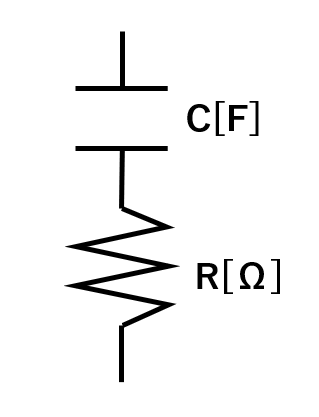
合成インピーダンスは、
$$Z=R+\frac{1}{jwC}$$
$$Z=R-j\frac{1}{wC}$$
になる。
なので合成アドミタンスは逆数を取って、
$$\color{red}{Y=\frac{1}{R-j\frac{1}{wC}}}$$
一応整理して、有理化した場合の値も下に書いておきます。
$$\color{red}{Y=\frac{R+j\frac{1}{wC}}{R^{2}+\frac{1}{(wC)^{2}}}}$$
では、合成アドミタンスを直接出すやり方だと、どうなるでしょうか?

これ、自分も含め、周りの人を見ていても、必ず一度は引っ掛かる間違いポイントがあるので、是非ここで実際に手を動かしてみて欲しいです。
アドミタンスを直接導出。
$$\frac{1}{Y}=R+\frac{1}{jwC}$$
なので、合成アドミタンスYは逆数を取って、
$$\color{red}{Y=\frac{1}{R+\frac{1}{jwC}}}$$
一致しました。式は非常にシンプルです。
しかし一度手を動かした人の中には、
$$\frac{1}{Y}=\frac{1}{R}+jwC$$
とやってしまった人も多くいると思います。
アドミタンスはインピーダンスに比べて使う機会が少ないため、こういった凡ミスが起こりやすいです。
直列の合成アドミタンスを考えたい場合には、インピーダンスを考えてから逆数を取るという意識を植え付けておきましょう!
ポイント(再掲)
直列接続の合成アドミタンスを解く際は、まず合成インピーダンスを求めるべし!
【パターン④】並列回路のインピーダンス。
最後に並列回路のインピーダンスを考えます。
条件
\(Z_1=R_1+jX_1\)と\(Z_2=R_2+jX_2\)の素子が並列で接続されたときの合成インピーダンスを求める。

並列接続の合成インピーダンスの式は、
$$\frac{1}{Z}=\frac{1}{Z_1}+\frac{1}{Z_2}$$
なので、まずはそれぞれの回路のインピータンスを考えます。
それぞれのインピーダンスは、
$$\frac{1}{Z_1}=Y_1$$
$$\frac{1}{Z_2}=Y_2$$
となります。
並列回路のインピーダンスの式に代入すると、
$$\frac{1}{Z}=Y_1+Y_2$$
となりますよね。
なので、合成インピーダンスは、
$$\color{red}{Z=\frac{1}{Y_1+Y_2}}$$
で表せます。

直列接続の合成アドミタンスと違い、こっちのパターンは問題演習等でも比較的よく扱うと思うので、そこまで違和感はないはずです。
ただ集中力を欠いていると、最後にインピーダンスに直す際に、逆数を取り忘れるミスが起こります。
イコールで式を繋げるときは、今何を考えているのかを意識しましょう!
例題4
下図のように、\(R[Ω]\)の抵抗と\(C[F]\)のコンデンサと\(L[H]\)のコイルをつないだときの合成インピーダンスを求めよ。
ただし、電源は交流電圧源とし、周波数はωとする。

求める合成インピーダンスZは、
$$\frac{1}{Z}=\frac{1}{R+jwL}+\frac{1}{\frac{1}{jwC}}$$
$$\frac{1}{Z}=\frac{1}{R+jwL}+jwC$$
$$\frac{1}{Z}=\frac{R-jwL}{R^{2}+(wL)^{2}}+jwC$$
なので整理して、
$$\frac{1}{Z}=\frac{R}{R^{2}+(wL)^{2}}+jw(C-\frac{L}{R^{2}+(wL)^{2}})$$
よって合成インピーダンスZは逆数を取って、
$$Z=\frac{1}{\frac{R}{R^{2}+(wL)^{2}}+jw(C-\frac{L}{R^{2}+(wL)^{2}})}$$
まとめ
ということで今回の記事では、インピーダンスとアドミタンスに関して、直列接続と並列接続の特徴をみてきました。
まとめ
・直列回路ではインピーダンスを、並列回路ではアドミタンスを考えると良い。
ぜひこのことを頭に入れて、電気回路の問題演習に取り組んでみてください!