

こんにちは、カイトです。
この記事では、自由空間と導体が作る静電界の違いを同じ球対称での電荷分布を取り扱いながら比較していこうと思います!
この記事で学べること。
・ガウスの法則の基本的な導出がわかる。
・静電界の違いがわかる。
目次
静電界とは?
この違いを考えるうえでまず大切になってくるのが、
静電界ってなんだ?
ということです。
静電界
静電界は、時間的に変化しない場合での電界のこと。
ここで重要となってくるのは、電界ということです。
この記事でこれから解説していきたいのは、自由空間と導体では生じる電界が違う!ということです。
今回は、この2パターンについて、生じる電界を比較することで静電界の違いを解説していきます。
取り扱う2つの空間。
①自由空間に、半径Rの球状に体積電荷密度ρで一様に分布している電荷が作る電界。
②半径Rの導体球に分布した電荷Qが作る電界。
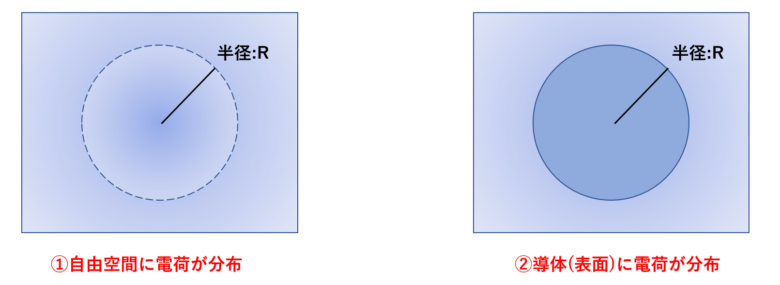

電磁気の問題演習をしていると、必ず一度は目にする問題設定だと思います!
この一見似ている、2つの場合の電界をそれぞれ考えていきます。
自由空間における静電界
まずは、1つ目の自由空間上に分布した電荷の作る電界を考えます。
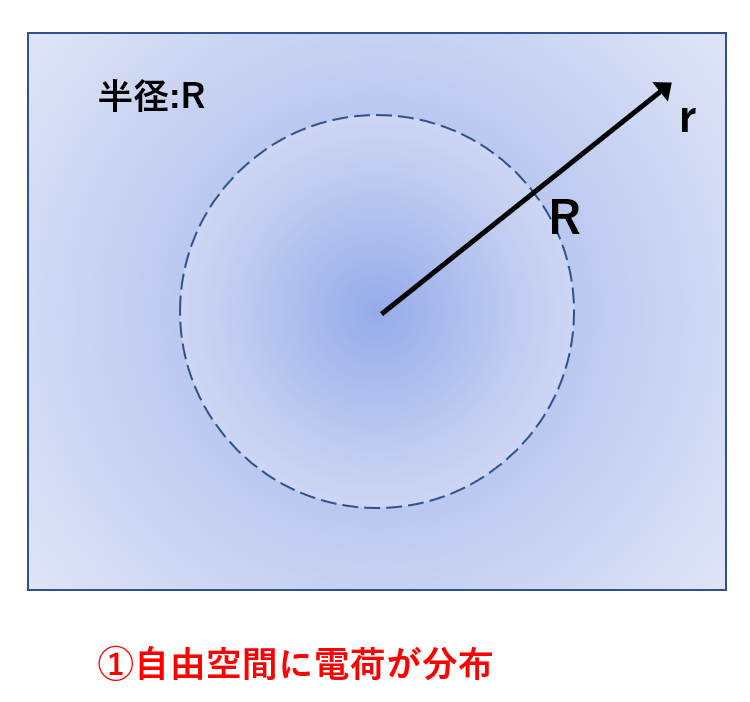
電界は、球の内部なのか、外部なのかで変わるので、場合分けをします。
ここで球の中心からの距離をrと置きます。
0<r<Rのとき
この時、ガウスの法則を考えると以下の式を得ます。
(ここで、閉空間内に存在する電荷をQ’と置きます。)
ガウスの法則
$$\left.\oint E・dS=\frac{Q’}{ε_0}\right.$$
$$Q’=ρ・\frac{4πr^{3}}{3}$$
この式を整理して、Eの式として表すと、
$$E・4πr^{2}=ρ・\frac{4πr^{3}}{3ε_0}$$
$$E=\frac{ρ}{3ε_0}・r\tag{1}$$
であるとわかります。
R<rのとき
同様に、ガウスの法則から電界を考えていきます。
ガウスの法則(再掲)
$$\left.\oint E・dS=\frac{Q’}{ε_0}\right.$$
$$Q’=ρ・\frac{4πr^{3}}{3}$$
R<rの場合は、閉曲面内にすべての電荷が存在しており、Q’は一定の値になる。
r=Rを代入して、Q’は以下の値になる。
$$Q’=ρ・\frac{4πR^{3}}{3}$$
ここから、同様に式を整理していくと、
$$E・4πr^{2}=ρ・\frac{4πR^{3}}{3ε_0}$$
$$E=\frac{ρR^{3}}{3ε_0}・\frac{1}{r^{2}}\tag{2}$$
電界とグラフ。
(1)と(2)の式から以下の結果を得ます。
電界
$$E=\frac{ρ}{3ε_0}・r (0<r<R)$$
$$E=\frac{ρR^{3}}{3ε_0}・\frac{1}{r^{2}} (R<r)$$
最後に関係をグラフに表しておきましょう。
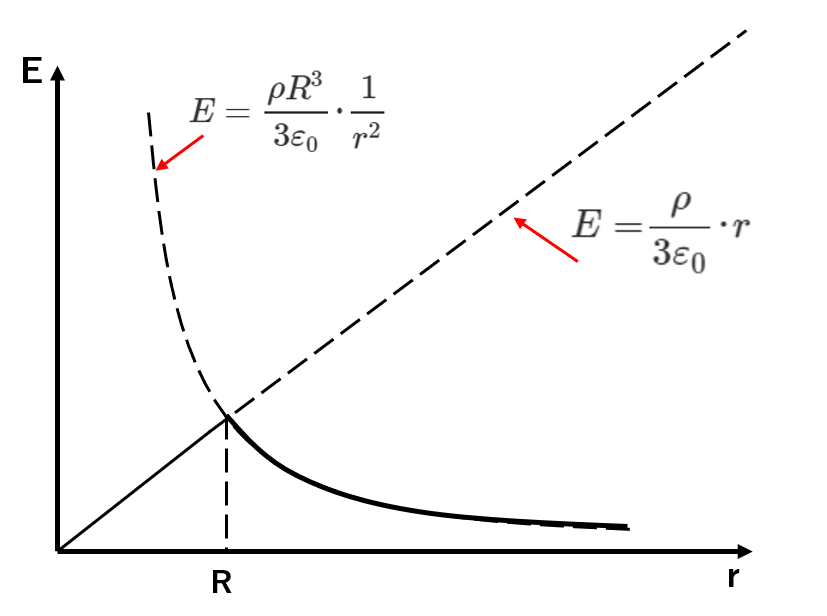
上の図でもわかるように、すべてのrにおいて連続的に電界が存在していることがわかります。
導体における静電界
続いて半径Rの導体球に分布した電荷Qが作る電界を考えます。
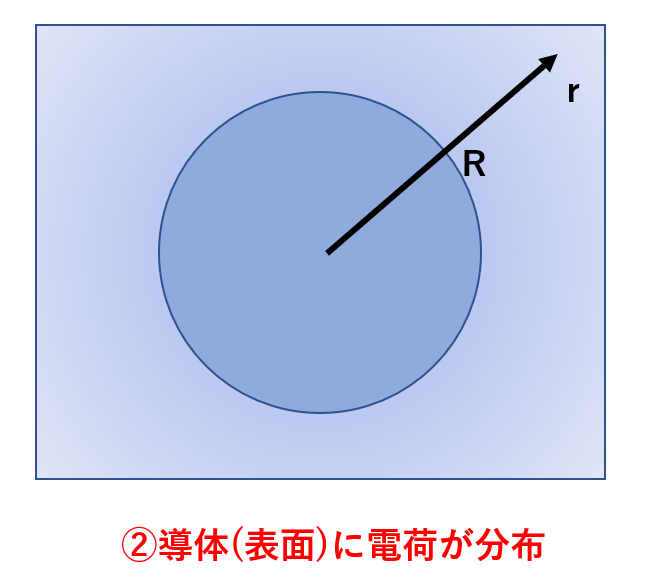
ここでも導体球の中心からの距離をrとして、rの範囲で場合分けをします。
0<r<Rのとき
導体球に電荷を分布したとき、導体球内部には電荷が存在せず、球面に一様に分布します。
つまり、導体球内部には電荷が存在しないため、電界Eはゼロになります。
ポイント
導体球内部には電荷が分布せず、電界が存在しない。
$$E=0\tag{3}$$
R<rのとき
ガウスの法則より、
$$E=\frac{Q}{4πε_0r^{2}}\tag{4}$$
ガウスの法則(再掲)
$$\left.\oint E・dS=\frac{Q}{ε_0}\right.$$
r=Rのとき
r=Rの内部は導体で外部は自由空間になっていて、r=Rがちょうど境界になっています。
このとき、導体表面の電界はクーロンの定理から、
$$E=\frac{Q}{4πε_0R^{2}}\tag{5}$$
とわかる。
クーロンの定理
導体表面に面電荷密度ρsで電荷が分布するとき、その表面での電界は、
$$E=\frac{ρ_0}{ε_0}$$
で与えられる。これをクーロンの定理という。
電界とグラフ。
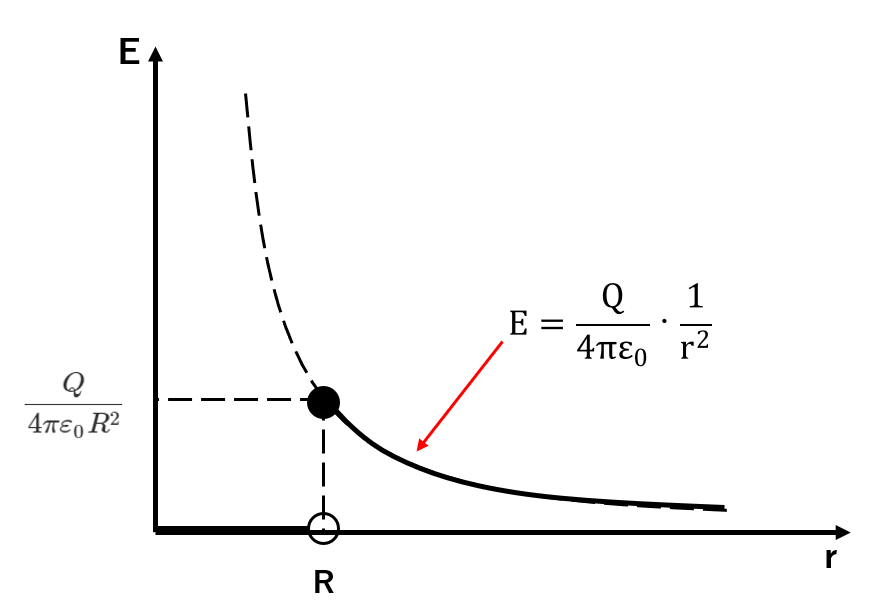
以上より、電界は以下のように表されます。
電界
$$E=0 (0<r<R)$$
$$E=\frac{Q}{4πε_0r^{2}} (R≦r)$$
グラフで表すと、下のようになります。
2つの空間内における電界の違い。
自由空間における電界と、自由空間内に置いた導体が作る電界を並べてみてみます。
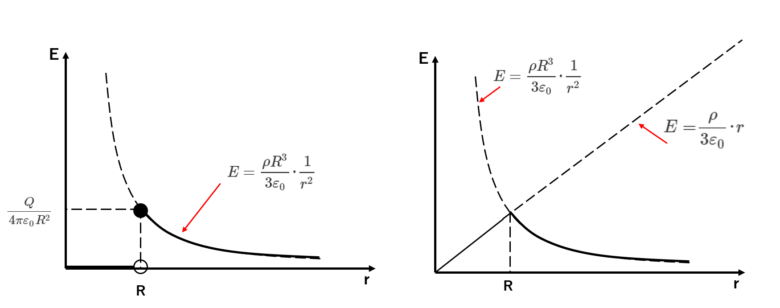
ポイント
・自由空間内(R≦r)での電界分布は等しい!
・自由空間では、連続的に電界が分布される。
・導体内の電界はゼロである。
今回取り上げた2つのパターンに関して、このように比較することはほぼないと思います。
比較してみるとこんな違いがあるのだなと是非わかってもらえると嬉しいです!
まとめ。
ということで今回は空間における電界分布の違いをみてみました。
まとめ
・空間の違いによって電荷分布は異なる!
今回の扱った1つ1つの現象は、当たり前のことでこの記事を読んでいる人の多くは理解できているはずです。
ただ、静電界を考える際の空間の認識が甘い人はいるはずです。
是非この記事を参考に、空間によって電界が異なる!ということを頭に入れておきましょう!