
こんにちは、カイトです。
この記事では、アドミタンスについて基本的な性質と考え方について解説していきます。
この記事でわかること。
・アドミタンスについての理解が深まる。
・アドミタンスの並列・直列接続の違いがわかる。
アドミタンスとは?
まずはアドミタンスについて解説します。
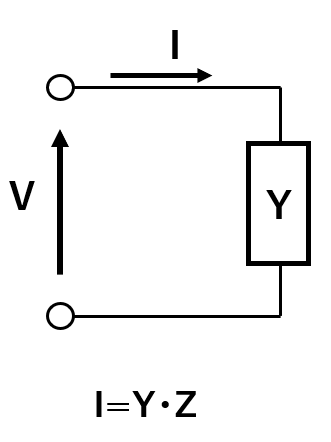
アドミタンス
上の図の二端子回路における電圧と電流の関係を表す複素数Yのことアドミタンスという。
$$I=Y・V$$
で表すことができる。
また、インピーダンスZを用いると、
$$Y=\frac{1}{Z}$$
とも表せる。
なお、アドミタンスの単位は[S(ジーメンス)]を用いる。これは、[Ω]の逆数にあたる。
アドミタンスは複素数であらすことができ、一般的に実部(コンダクタンス)を\(G\)で、虚部(サセプタンス)を\(B\)を用いて、
$$\color{red}{\dot{Z}=G+jB}$$
で表すことができます。
アドミタンスはとインピーダンスは並列に取り扱うことができるので、両者を合わせてイミタンスと呼びます。
メモ
インピーダンスとアドミタンスの相互関係については以下の記事についてまとめています。
併せて確認してみてください!
アドミタンスに関して重要なのは、ベクトル線図で考えたときに基準が電圧であることです。
電気回路のベクトル図表示
一般的な回路において、電流と電圧の間には大きさの違いと位相差が生じます。
この違いをインピーダンスZを使って表すことができるわけですが、僕たちがあくまで知りたいのは大きさの違いと位相差なわけです。
この、特徴的な二つの変数(大きさ/位相差)を一目でわかるように可視化したものがベクトル図になります。
$$I=YV$$
に関して、この式を解釈すると、
電圧フェーザVにアドミタンスYをかけると、電流フェーザIが求まる
ということがわかります。
メモ
フェーザ表示に関しては、下の記事でまとめています。
是非合わせて確認してみて下さい!
ベクトル図で表すと下のようになります。
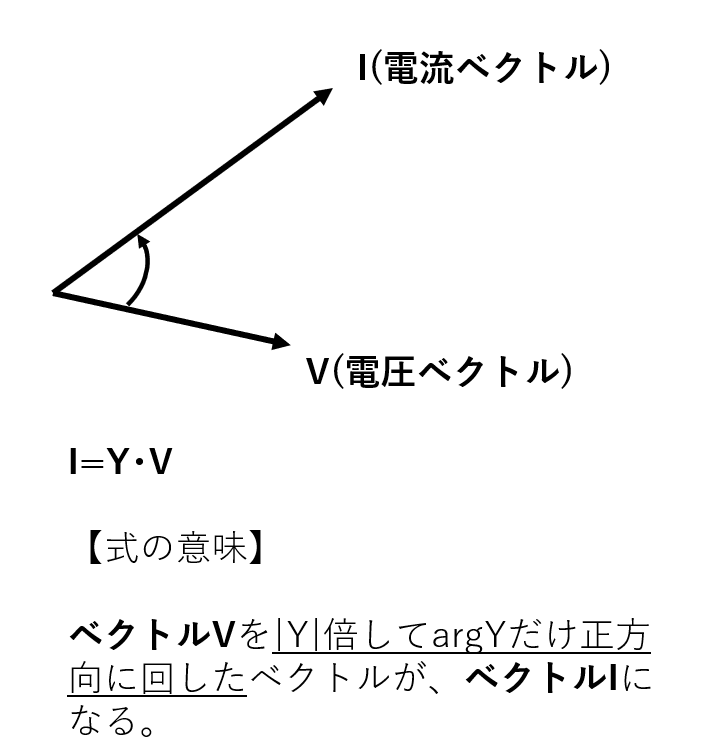

この、基準が電圧ベクトルである、ということが回路の遅れや進みを考えていく上で非常に重要になっていくのでしっかり頭に入れて置きましょう。
それではここから具体的なアドミタンスの接続方法における特徴について、みていきます!
アドミタンスの直列接続
まずはアドミダンスの直列接続です。
アドミダンスの直列接続
二つのアドミタンス\(Y_1\)と\(Y_2\)を直列につないだときの、合成インピーダンスは、
$$\color{red}{\frac{1}{Y}=\frac{1}{Y_1}+\frac{1}{Y_2}}$$
で表せる。
この等式を証明するために下の図を用います。
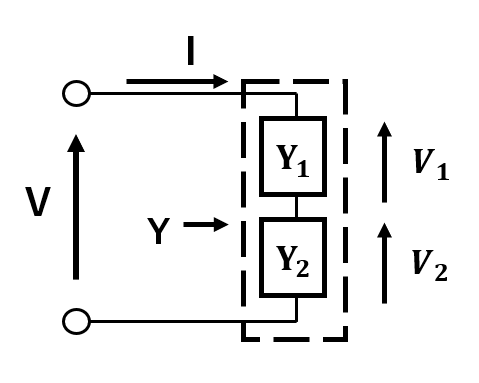
ここで、フェーザ表示における、電流と電圧の式を考えれば、
$$V_1=\frac{I}{Y_1}$$
$$V_2=\frac{I}{Y_2}$$
$$V=V_1+V_2$$
の3式を得ます。
ここで、それぞれの式から、\(V_1\)と\(V_2\)を消去すると、
$$V=(\frac{1}{Y_1}+\frac{1}{Y_2})・I$$
この\(\frac{1}{Y_1}\)と\(\frac{1}{Y_2}\)の和を\(\frac{1}{Y}\)で表すことで、直列回路全体の合成アドミタンスが求まります。
$$\color{red}{\frac{1}{Y}=\frac{1}{Y_1}+\frac{1}{Y_2}}$$
メモ
インピーダンスZを用いて直列接続の式を表すと、それぞれの項の逆数を取ればいいので
$$Z=Z_1+Z_2$$
を得ます。
導出は下の記事を参考にしてください!
アドミタンスの並列接続
続いて、アドミタンスの並列接続を考えます。
アドミタンスの並列接続
二つのアドミタンス\(Y_1\)と\(Y_2\)を並列につないだときの、合成アドミタンスは、
$$\color{red}{Y=Y_1+Y_2}$$
で表せる。
この等式を証明するために下の図を用います。
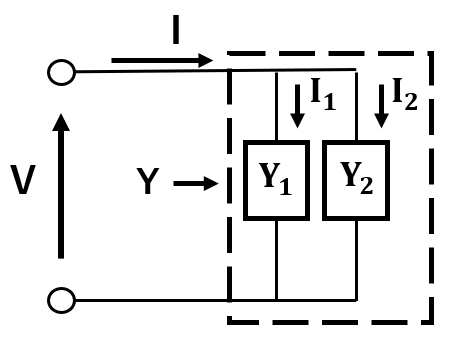
ここで、フェーザ表示における、電流と電圧の式を考えれば、
$$I_1=Y_1・V$$
$$I_2=Y_2・V$$
$$I=I_1+I_2$$
の3式を得ます。
ここで、それぞれの式から\(I_1\)と\(I_2\)を消去すると、
$$I=(Y_1+Y_2)・V$$
と表せます。
この\(Y_1\)と\(Y_2\)の和をYで表すことで、並列回路全体の合成アドミタンスが求まります。
$$\color{red}{Y=Y_1+Y_2}$$
メモ
インピーダンスZを用いて並列接続の式を表すと、それぞれの項の逆数を取ればいいので
$$\frac{1}{Z}=\frac{1}{Z_1}+\frac{1}{Z_2}$$
を得ます。
導出は下の記事を参考にしてください!
まとめ
ということでこの記事では、アドミタンスの性質と直列・並列接続の形を見ていきました。
まとめ
・アドミタンスは、\(\color{red}{I=Z・V}\)で表せる。
・アドミタンスの直列接続は、\(\color{red}{\frac{1}{Y}=\frac{1}{Y_1}+\frac{1}{Y_2}}\)で表せる。
・アドミタンスの並列接続は、\(\color{red}{Y=Y_1+Y_2}\)で表せる。
是非この記事を参考にアドミタンスについての理解を深めていきましょう!